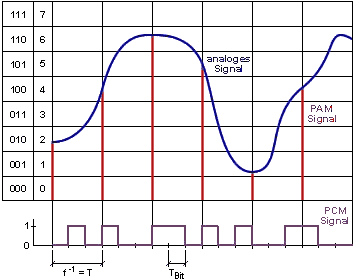
Nesse post iremos fazer uma simulação de um sistema PCM no Matlab ou Octave. Essa simulação foi feita para o trabalho final da disciplina de Sistemas de comunicação 1.
A simulação é composta pelas seguintes etapas de:
- amostragem;
- quantização com compressor lei µ;
- codificação PCM.
O algoritmo desenvolvido deve segue o seguinte fluxograma:

Para a etapa de amostragem, utilizamos como referência o código PAM. O código implementado tem como parâmetros variáveis: a taxa de amostragem (fs); Largura do pulso PAM; a resolução de quantização (B); o parâmetro de compressão (µ); e a largura de pulso PCM (TPCM). O sinal e algumas variáveis é carregada pelo arquivo sinal.mat (posso mandar por email, comente pedindo.)
SIMULAÇÃO
clc; %limpa console
clear all; % Apaga as variaveis e funcoes
close all; % Fecha as figuras das janelas
load ('sinal.mat'); %Le o sinal banda base e algumas variaveis
O código acima carrega o sinal, limpa console, variáveis e gráficos.
%*************************
% Definindo Parametros *
%*************************
freqAmostragem = 50; %Frequencia de amostragem
U= 255; %Parametro de compressao Lei A
B = 8; %Parametro do quantizador (bits)
Tb = 2; %Periodo de bit
Tpam = 0.4;
Tpcm = 1e-7; %Largura de pulso = 1e-7
t = (0:1:size(m,2)-1)*T; %Gerando vetor de tempo
Mostra o o sinal carregado em função do tempo e seu espectro.
%*************************
% Sinal Original *
%*************************
subplot(4,1,1);
plot(t, m); % Plotar o sinal
grid on;
title ('Sinal no dominio do tempo m(t)');
xlabel('Tempo');
ylabel('Amplitude');
%APLICANDO TRANSFORMADA DE FOURIER NO SINAL
X = fftshift(abs(fft(m))); %Aplica a transformada de fourier no sinal
subplot(4,1,2);
plot(X); %Plotar o sinal com a transformada
grid on;
title('Espectro do sinal m(t) na frequencia');
xlabel('Frequencia (hz)');
ylabel('Amplitude');
Amostra o sinal carregado e o mostra em função do tempo e seu espectro.
%*************************
% Amostragem *
%*************************
sinal = m; %Carrega o sinal e armazena em uma variavel
tamSinal = length(sinal);
Tam = 1/freqAmostragem;
quantPulsos = ceil(Tam / T); %arredonda
for i=1:quantPulsos:tamSinal
ms(1,i)= m(1,i);
end
subplot(4,1,3);
plot(ms); % plota amostrado
grid on;
title('Sinal Amostrado');
xlabel('Tempo');
ylabel('Amplitude');
%Espectro do sinal Amostrado
expectroMs = fftshift((fft(ms)));
tam2 = max(size(expectroMs));
f2 = [-(fs/2):fs/(tam2-1):fs/2];
subplot(4,1,4);
plot(f2,abs(expectroMs)); %Plotar o sinal de amostragem
grid on;
title('Espectro do Sinal Amostrado na frequencia');
xlabel('Frequencia (hz)');
ylabel('Amplitude');
Modula o sinal amostrado na amplitude convoluindo as amostras com o trem de pulsos e o mostra em função do tempo e seu espectro. Lembrando que usamos a compressão µ, se precisar usar a compressão A, muda-se apenas a equação. No código a seguir, há também parte de normalização de 1 a -1 e 1 a 0. Essa parte é necessária dependendo do estilo de quantização e codifição que irá usar.
%*************************
% PAM *
%*************************
Lpam = Tpam*quantPulsos; %Gerando sinal PAM atraves da convolucao do sinal ms com pulso ret
h = ones(1,Lpam); %vetor de pulso retangular
spam = conv(ms,h); %spam = amostra*h
figure(2);
subplot(4,1,1);
plot(spam); %plotar o sinal PAM
grid on;
title('Sinal PAM');
xlabel('Tempo');
ylabel('Amplitude');
%normaliza -1 a 1
max_spam=max(spam);
min_spam=min(spam);
y = ((2.*(spam-max_spam))./(max_spam-min_spam))+1;
%Compressao do sinal PAM usando LEI MI
y1=((log10(1+(U.* abs(y))))./log10(1+U)).* sign(y);
%Vetor de tempo
t=(0:1:size(y1,2)-1)*T;
%Mostra o sinal PAM apos a compressao
subplot(4,1,2);
plot(t,y1);
grid on;
title('Sinal PAM Comprimido');
xlabel('Tempo');
ylabel('Amplitude');
%normaliza 0 a 1
max_n=max(y1);
min_n=min(y1);
y1 = (((y1-max_n))./(max_n-min_n))+1;
subplot(4,1,3);
plot(t,y1); %Mostra o sinal normalizado 0 a 1
grid on;
title('Sinal PAM Comprimido e Normalizado de 0 a 1');
xlabel('Tempo');
ylabel('Amplitude');
%Espectro do Sinal PAM na frequencia
expPam=fftshift(fft(y1)); %Gera a Transformada de Fourier do Sinal PAM
tam3 = max(size(expPam)); %vetor de frequencia 3
f3 = [-(fs/2):fs/(tam3-1):fs/2];
subplot(4,1,4);
plot(f3,abs(expPam)); %Mostra a Transformada de Fourier do Sinal PAM
grid on;
title('Espectro do Sinal PAM');
xlabel('Frequencia(Hz)');
ylabel('Amplitude');
Quantiza o sinal e o mostra em função do tempo e seu espectro.
%**********************
% QUANTIZAÇÃO *
%**********************
%Processo de Quantizacao
nivel = 2^B; % resolucao em bits
Vmax = nivel/2;
Vmin = (nivel/2)-1;
x1 = Vmax.*y1;
x2 = Vmin.*y1;
q = round(x1)+ round(x2); %Arrendondamento
figure(3);
subplot(2,1,1);
plot(t,q); %Mostra o Sinal Quantizado
grid on;
title('Sinal Quantizado');
xlabel('Tempo');
ylabel('Amplitude');
%Espectro do Sinal Quantizado
espQ=fftshift(fft(q));
%vetor de frequencia 4
tam4=max(size(espQ));
f4=[-(fs/2):fs/(tam4-1):fs/2];
subplot(2,1,2);
plot(f4,abs(espQ)); %Mostra a Transformada de Fourier do Sinal Quantizado
grid on;
title('Espectro do sinal quantizado Final');
xlabel('Frequencia(Hz)');
ylabel('Amplitude');
Codifica o sinal quantizado no código de linha Bipolar sem retorno a zero. Para demonstrar usamos apenas a primeira amostra do sinal quantizado. Para mais, basta incrementar um pequeno código para codificar as N amostras.
%************************************
% CODIFICAÇÃO PCM NRZ BIPOLAR *
%************************************
h = dec2bin(q(1))-'0'; %Primeira amostra 169 convertida em vetor de binario
n=1;
l=length(h);
h(l+1)=1;
figure(4);
while n<=length(h)-1;
t=n-1:0.001:n;
if h(n) == 0
if h(n+1)==0
y=-(t<n)-(t==n);
else
y=-(t<n)+(t==n);
end
d=plot(t,y);grid on;
title('Line code BIPOLAR NRZ');
set(d,'LineWidth',2.5);
hold on;
axis([0 length(h)-1 -1.5 1.5]);
disp('zero');
else
if h(n+1)==0
y=(t<n)-1*(t==n);
else
y=(t<n)+1*(t==n);
end
d=plot(t,y);grid on;
title('Line code BIPOLAR NRZ');
set(d,'LineWidth',2.5);
hold on;
axis([0 length(h)-1 -1.5 1.5]);
disp('one');
end
n=n+1;
end
Acabou! Deu certo ai? Comente ;)









0 comentários:
Postar um comentário